Pythonではじめてのマクローリン展開

2022-02-17•Python

cover image from Unsplash

本記事の内容

Python の sympy を用い、指数関数 $f(x)=e^{x}$ のマクローリン展開を計算する。
得られた式を matplotlib でグラフ表示する。

マクローリン展開する関数

指数関数 $f(x)=e^{x}$ のマクローリン展開を以下に示す。

\begin{aligned} e^{x} &= \displaystyle\sum_{n=0}^\infin{x^{n} \above{1pt} n!} \\ &= 1 + x + {1 \above{1pt} 2} x^{2} + {1 \above{1pt} 6} x^{3} + {1 \above{1pt} 24} x^{4} + \cdots \end{aligned}

sympy でマクローリン展開

sympy のドキュメントはこちら。

Symbol について
Gotchas - SymPy 1.14.dev documentation

series（級数展開）について
Calculus - SymPy 1.14.dev documentation

コード1

from sympy import *
 
# 文字'x'を変数xとして定義
x = Symbol('x')
 
# 指数関数exp(x)を、第5項(n=5)までマクローリン展開（x0=0)
maclaurin = series(exp(x), x=x, x0=0, n=5)
print(maclaurin)
print(maclaurin.removeO())

出力結果1

1 + x + x**2/2 + x**3/6 + x**4/24 + O(x**5)
x**4/24 + x**3/6 + x**2/2 + x + 1

4 次の第 5 項までのマクローリン展開結果が出力された。 O(x**5)は、5 次以降の剰余項であり、.remove()で取り除くことができる。

マクローリン展開で得られた式を、グラフ表示する

上記の計算結果が $f(x)=e^{x}$ の近似になっているか確かめるために、numpy.exp()による計算結果も同一グラフ上にプロットする。

コード2

from sympy import *
import numpy as np
import matplotlib.pyplot as plt
 
# numpyで、指数関数exp(x)を計算
cal_x = np.arange(start=0, stop=10, step=1)
cal_y = np.exp(cal_x)
 
 
# 指数関数exp(x)を、n次の項(n=n)までマクローリン展開（x0=0)
def mac_y(n):
    x = Symbol('x')
    maclaurin = series(exp(x), x=x, x0=0, n=n).removeO() # 余剰項を取り除く
    maclaurin_y = lambdify(x, maclaurin, modules='numpy') # numpyに変換
    return maclaurin_y(cal_x)
 
 
# グラフ表示
plt.title("f(x) = exp(x)")
plt.plot(cal_x, mac_y(n=10), color='blue', label='Maclaurin') # 第10項(n=10)まで展開
plt.plot(cal_x, cal_y, color='orange', label='numpy.exp')
plt.legend()
plt.show()

出力結果2

第 10 項(n=10)までマクローリン展開した結果を以下に示す。

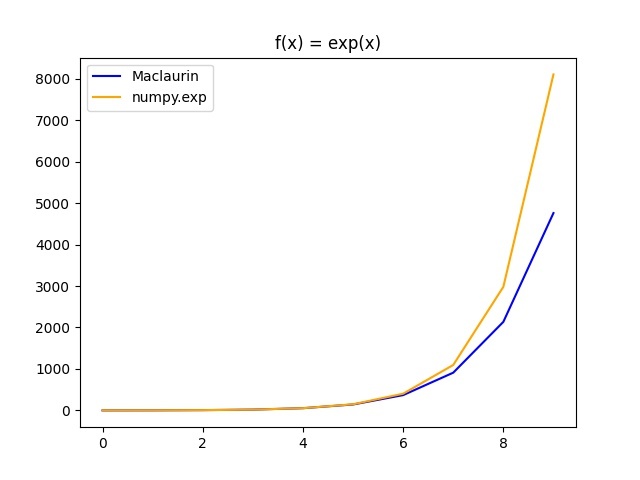
コード内の変数 n を変えることで、より $f(x)=e^{x}$ に近似した曲線グラフを得ることができる。例として、第 50 項(n=50)までマクローリン展開した結果を以下に示す。

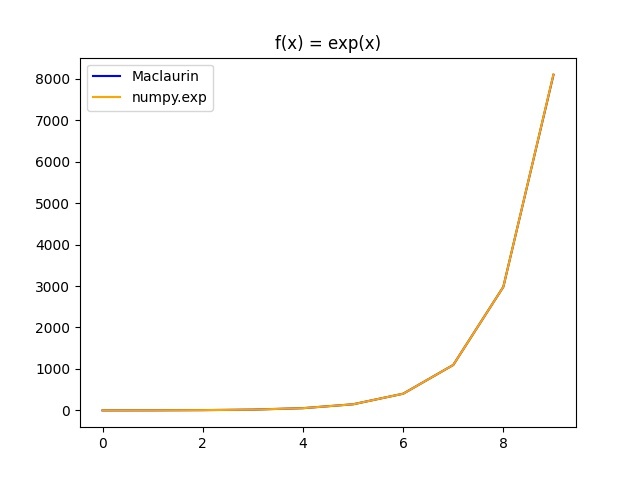
あとがき

アイキャッチ画像の緑のヘビさん、SymPy のヘビに似てないですか。世の中にはこんな可愛いらしいヘビもいるんですね。今後 SymPy 関連の記事を書くことがあれば、また使おうと思います。