数式を使わず,相互相関を理解しよう(Pythonソースコード付き)

Photo by Amir-abbas Abdolali on Unsplash
本記事について
本記事は,Python で相互相関(numpy.correlate(), scipy.signal.correlate())を行いたいが,そもそも相互相関をよく知らない人を対象に,ややこしい(?)数式は使わず様々な波形を図示することで,相互相関のイメージを持ってもらうことを目指している。
目次
- 相互相関(Cross-correlation)って何?
- 相互相関のイメージをつかもう
2-1. 正弦波(1 周期)
2-2. 正弦波(3 周期)
2-3. チャープ波 (1 周期)
2-4. チャープ波 (3 周期)
2-5. ランダム波
2-6. 正弦波(1 周期)に,ホワイトノイズが乗っている場合 - 相互相関って、具体的にどんな計算しているの?
1. 相互相関(Cross-correlation)って何?
相互相関関数(そうごそうかんかんすう、英: cross-correlation function)は、ふたつの信号、配列(ベクトル)の類似性を確認するために使われる。関数の配列の結果がすべて 1 であれば相関があり、すべてゼロであれば無相関であり、すべて −1 であれば負の相関がある。 相互相関関数(wikipedia より)
つまり、2 つの配列(今回の場合は波形)を比較する計算であり,
- 値が大きければ(正規化した場合、最大値は 1),両者は「似ている」
- 値が 0 に近ければ,両者は「似ていない」
ということになる。
なお,自己相関とは,同一波形同士で相互相関と同じ計算を行ったものである。
2. 相互相関のイメージをつかもう
送信波と受信波を想定し,両者の相互相関をとると,どんな結果が得られるか,色々シミュレーションしてみる。
2-1. 正弦波(1 周期)
import numpy as np
import matplotlib.pyplot as plt
n = 100
time1 = np.linspace(start=0, stop=2*np.pi, num=n)
sin1 = np.sin(time1)
time2 = np.linspace(start=0, stop=2*(2*np.pi), num=2*n)
sin2 = np.concatenate([np.zeros(n), sin1])
time3 = np.linspace(start=-2*np.pi, stop=2*(2*np.pi), num=n+(2*n)-1)
correlation = np.correlate(sin2, sin1, mode="full")
fig, ax = plt.subplots(3)
ax[0].plot(time1, sin1)
ax[1].plot(time2, sin2)
ax[2].plot(time3, correlation)
ax[0].text(0.2, -0.8, "wave1")
ax[1].text(0.2, -0.8, "wave2")
ax[2].text(0.2, 30, "cross-correlation")
ax[0].set_xlim(0, 2*2*np.pi)
ax[1].set_xlim(0, 2*2*np.pi)
ax[2].set_xlim(0, 2*2*np.pi)
fig.show()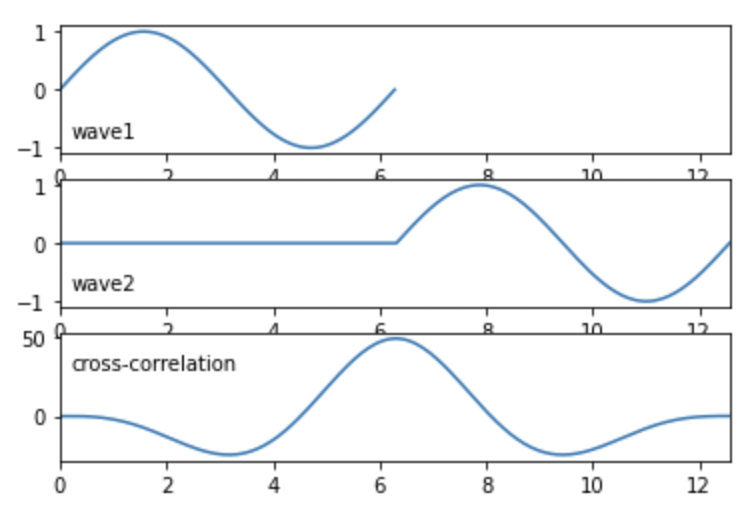 出力結果。
出力結果。
2-2. 正弦波(3 周期)
import numpy as np
import matplotlib.pyplot as plt
n = 100
time = np.linspace(start=0, stop=2*np.pi, num=n)
sin = np.sin(time)
time1 = np.linspace(start=0, stop=3*(2*np.pi), num=3*n)
sin1 = np.tile(sin, reps=3)
time2 = np.linspace(start=0, stop=2*(3*(2*np.pi)), num=3*(2*n))
sin2 = np.concatenate([np.zeros(3*n), sin1])
time3 = np.linspace(start=-3*(2*np.pi), stop=3*(4*np.pi), num=3*(n+(2*n))-1)
correlation = np.correlate(sin2, sin1, mode="full")
fig, ax = plt.subplots(3)
ax[0].plot(time1, sin1)
ax[1].plot(time2, sin2)
ax[2].plot(time3, correlation)
ax[0].text(0.2, -0.8, "wave1")
ax[1].text(0.2, -0.8, "wave2")
ax[2].text(0.2, 110, "cross-correlation")
ax[0].set_xlim(0, 2*(3*(2*np.pi)))
ax[1].set_xlim(0, 2*(3*(2*np.pi)))
ax[2].set_xlim(0, 2*(3*(2*np.pi)))
fig.show()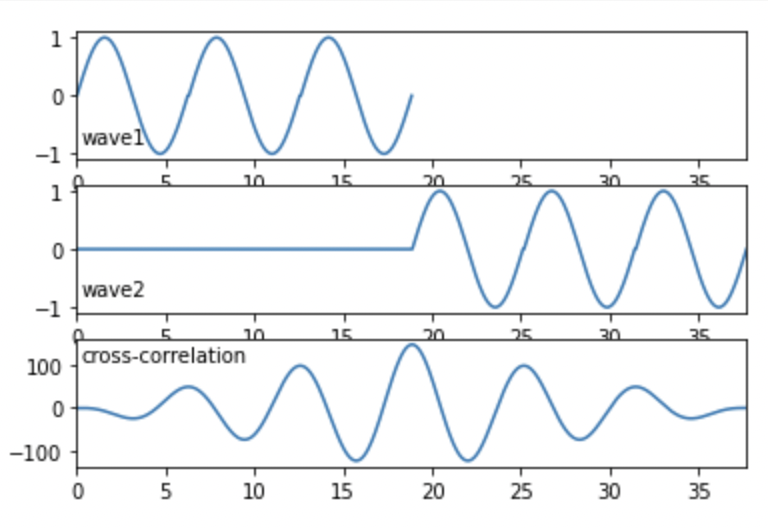 出力結果。
出力結果。
2-3. チャープ波
import numpy as np
import scipy.signal as signal
import matplotlib.pyplot as plt
n = 1000
time1 = np.linspace(start=0, stop=2*np.pi, num=n)
chirp1 = signal.chirp(time1, f0=1, t1=2*np.pi, f1=10, method='linear')
time2 = np.linspace(start=0, stop=2*(2*np.pi), num=2*n)
chirp2 = np.concatenate([np.zeros(n), chirp1])
time3 = np.linspace(start=-2*np.pi, stop=4*np.pi, num=n+(2*n)-1)
corr = np.correlate(chirp2, chirp1, mode="full")
fig, ax = plt.subplots(3)
ax[0].plot(time1, chirp1)
ax[1].plot(time2, chirp2)
ax[2].plot(time3, corr)
ax[0].text(0.2, -0.8, "wave1")
ax[1].text(0.2, -0.8, "wave2")
ax[2].text(0.2, 300, "cross-correlation")
ax[0].set_xlim(0, 2*2*np.pi)
ax[1].set_xlim(0, 2*2*np.pi)
ax[2].set_xlim(0, 2*2*np.pi)
fig.show()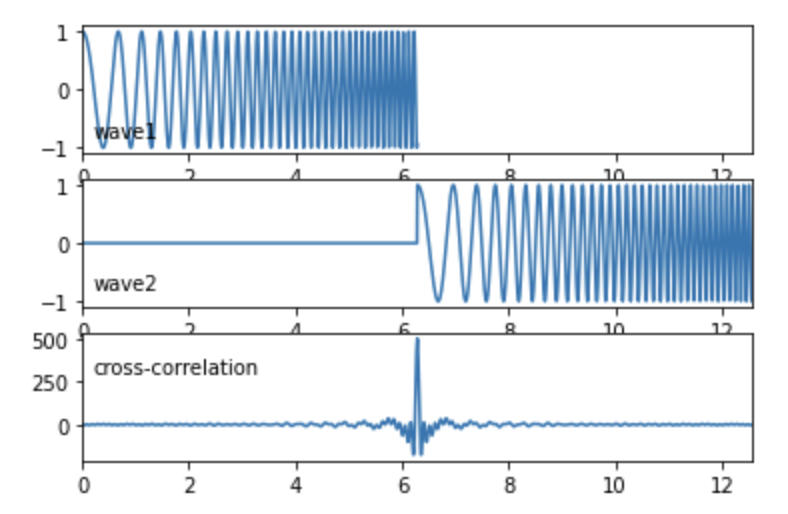 出力結果。
出力結果。
2-4. チャープ波(3 周期)
import numpy as np
import scipy.signal as signal
import matplotlib.pyplot as plt
n = 1000
time = np.linspace(start=0, stop=2*np.pi, num=n)
chirp = signal.chirp(time, f0=1, t1=2*np.pi, f1=10, method='linear')
time1 = np.linspace(start=0, stop=3*(2*np.pi), num=3*n)
chirp1 = np.tile(chirp, reps=3)
time2 = np.linspace(start=0, stop=3*(2*(2*np.pi)), num=3*(2*n))
chirp2 = np.concatenate([np.zeros(3*n), chirp1])
time3 = np.linspace(start=-3*(2*np.pi), stop=3*(4*np.pi), num=3*(n+2*n)-1)
corr = np.correlate(chirp2, chirp1, mode="full")
fig, ax = plt.subplots(3)
ax[0].plot(time1, chirp1)
ax[1].plot(time2, chirp2)
ax[2].plot(time3, corr)
ax[0].text(0.2, -0.8, "wave1")
ax[1].text(0.2, -0.8, "wave2")
ax[2].text(0.2, 300, "cross-correlation")
ax[0].set_xlim(0, 3*(2*2*np.pi))
ax[1].set_xlim(0, 3*(2*2*np.pi))
ax[2].set_xlim(0, 3*(2*2*np.pi))
fig.show()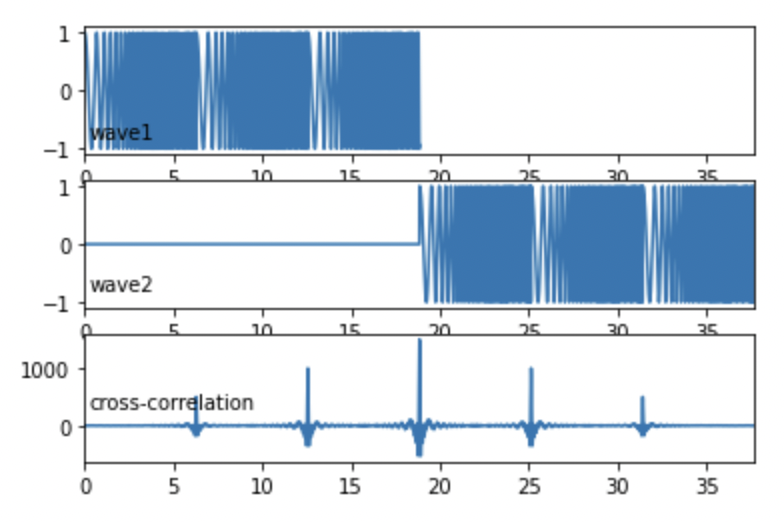 出力結果。
出力結果。
2-5. ランダム波
import numpy as np
import matplotlib.pyplot as plt
n = 100
time1 = np.arange(n)
rng = np.random.default_rng(seed=1)
random1 = rng.random(n) * 2 - 1
time2 = np.arange(2*n)
random2 = np.concatenate([np.zeros(n), random1])
time3 = np.linspace(start=-n, stop=2*n, num=n+2*n-1)
corr = np.correlate(random2, random1, mode="full")
fig, ax = plt.subplots(3)
ax[0].plot(time1, random1)
ax[1].plot(time2, random2)
ax[2].plot(time3, corr)
ax[0].text(0.2, -1, "wave1")
ax[1].text(0.2, -0.8, "wave2")
ax[2].text(0.2, 20, "cross-correlation")
ax[0].set_xlim(0, 2*n)
ax[1].set_xlim(0, 2*n)
ax[2].set_xlim(0, 2*n)
fig.show()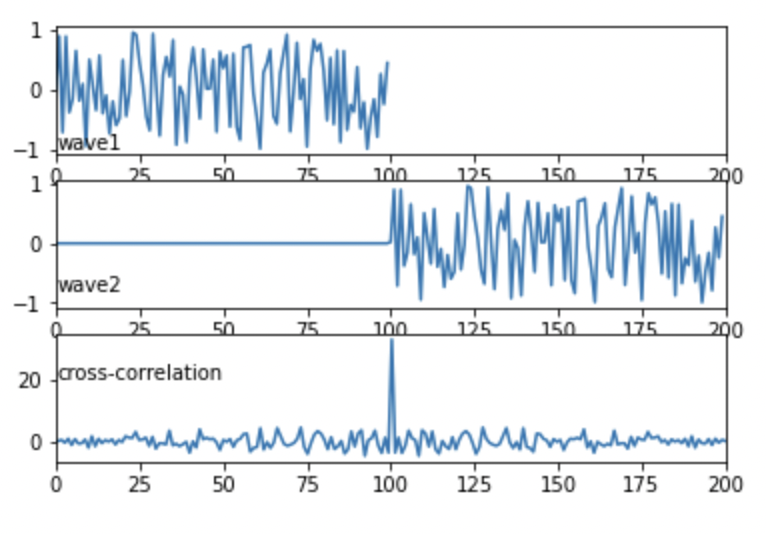 出力結果。
出力結果。
2-6. 正弦波(1 周期)に,ホワイトノイズが乗っている場合
import numpy as np
import matplotlib.pyplot as plt
n = 100
time1 = np.linspace(start=0, stop=2*np.pi, num=n)
sin1 = np.sin(time1)
time2 = np.linspace(start=0, stop=2*(2*np.pi), num=2*n)
rng = np.random.default_rng(seed=1)
random = rng.random(2*n) * 2 - 1
sin2 = np.concatenate([np.zeros(n), sin1]) + random
time3 = np.linspace(start=-2*np.pi, stop=2*(2*np.pi), num=n+(2*n)-1)
correlation = np.correlate(sin2, sin1, mode="full")
fig, ax = plt.subplots(3)
ax[0].plot(time1, sin1)
ax[1].plot(time2, sin2)
ax[2].plot(time3, correlation)
ax[0].text(0.2, -0.8, "wave1")
ax[1].text(0.2, -1.8, "wave2")
ax[2].text(0.2, 30, "cross-correlation")
ax[0].set_xlim(0, 2*2*np.pi)
ax[1].set_xlim(0, 2*2*np.pi)
ax[2].set_xlim(0, 2*2*np.pi)
fig.show()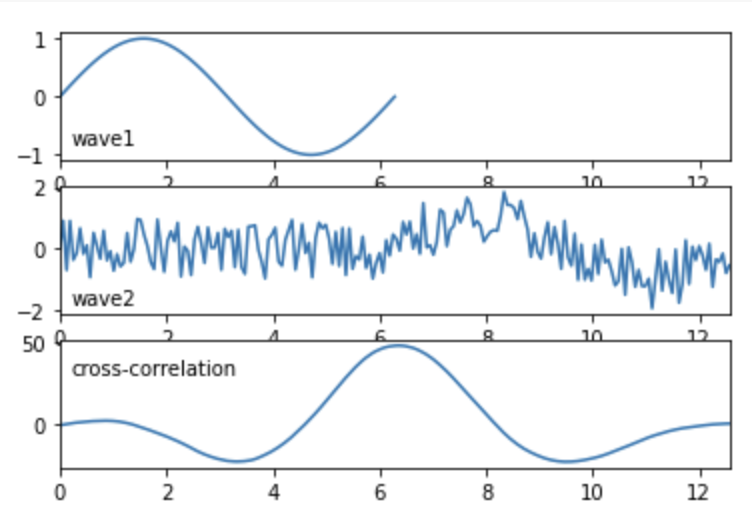 出力結果。
出力結果。
3. 相互相関って,具体的にどんな計算しているの?
以下の 2 つの離散値データ(波形 1,波形 2)について考える。
- 波形 1: (1, 2, -1, 0)
- 波形 2: (0, 2, 4, -2)
波形 1 は,
0 秒の時: 1
1 秒の時: 2
2 秒の時: -1
3 秒の時: 0
という値を持つサンプリング間隔 1 秒の配列である。
波形 1
| 0 | 1 | 2 | 3 | [秒] |
|---|---|---|---|---|
| 1 | 2 | -1 | 0 |
波形 2
| 0 | 1 | 2 | 3 | [秒] |
|---|---|---|---|---|
| 0 | 2 | 4 | -2 |
波形 1 と波形 2 を見比べると,
波形 2 は,波形 1 を 1 秒遅らせて,振幅が 2 倍になったものであり、
両者は,波形の到達時刻と振幅が異なるものの,波形の形状は同じ(=相関がある)であることがわかる。
これを念頭に置いて,
以下の波形 2 と波形 1 の相互相関の計算表をみてみる。
| -3 | -2 | -1 | 0 | 1 | 2 | 3 | 相互相関の計算 | 計算結果 | 遅れ時間 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 波形 2 | 0 | 2 | 4 | -2 | |||||||
| 波形 1 | 1 | 2 | -1 | 0 | 0*0 = 0 | 0 | -3 | ||||
| 1 | 2 | -1 | 0 | 0*(-1) + 2*0 = 0 | 0 | -2 | |||||
| 1 | 2 | -1 | 0 | 0*2 + 2*(-1) + 4*0 = -2 | -1 | 1 | |||||
| 1 | 2 | -1 | 0 | 0*1 + 2*2 + 4*(-1) + (-2)*0 = 0 | 0 | 0 | |||||
| 1 | 2 | -1 | 2*1 + 4*2 + (-2)*(-1) = 12 | 12 | 1 | ||||||
| 1 | 2 | 4*1 + (-2)*2 = 0 | 0 | 2 | |||||||
| 1 | (-2)*1 = -2 | -2 | 3 |
ポイントは,以下の 4 つである。
- 波形 2 を起点に,波形 1 が波形 2 と似ているか,一要素ずつずらしながらみていく
- 相互相関の値は,両波形の各要素ごとの掛け算の総和であらわされる
- 波形が同じ形をしている(=相関がある)ときは,+同士、-同士の掛け算になるため,総和は著しく大きくなる
- 一方,波形が異なる(=相関がない)ときは,総和は小さくなる
また,「波形 2 と波形 1 の相互相関」と,「波形 1 と波形 2 の相互相関」では,結果が同一にならない。
両者には,以下の表のような関係がある。
| 波形 2 と波形 1 の相互相関結果 | 遅れ時間 | 波形 1 と波形 2 の相互相関結果 |
|---|---|---|
| 0 | -3 | -2 |
| 0 | -2 | 0 |
| -2 | -1 | 12 |
| 0 | 0 | 0 |
| 12 | 1 | -2 |
| 0 | 2 | 0 |
| -2 | 3 | 0 |
まとめ
Python では,相互相関のライブラリ(numpy.correlate(), scipy.signal.correlate())があり,誰でも簡単に高速な相互相関処理が行えるが,そもそもどういった計算を行なっているのかよく理解していないと,出力される結果があっているのかどうかわからないという状況に陥ってしまう(以前の私のことです)。 この記事が,(以前の私のような)信号処理初心者の役に立てば幸いである。